It’s good to see @srcav back in the twitter and blogging fold - he’s been missed!

As part of his comeback, he shared this lovely geometry puzzle:

Circle/triangle puzzle

Assuming the situation is symmetrical (which it needs to be to get a sensible solution), there are - as usual - several ways to solve it. Like Cav, I went the messy way first; however, I wanted to share a related solution using the power of complex numbers - and (much later) one that comes directly from a little-used circle theorem.

Suppose the set-up is an Argand diagram

  • The ‘vector’ representing the left leg of the triangle corresponds to the complex number $z = 1 + \sqrt{2}i$.

  • Because we have a unit semicircle, the radius in the same direction is $\hat z = \frac{1}{\sqrt{3}}\br{1 + \sqrt{2}}$.

  • Because of the circle theorem about angles at the centre subtending double the angle at the circumference, we need to double the angle between the $x$-axis and $\hat z$ to find the intersection point, which we can do by squaring $\hat z$: we get $\frac{1}{3}\br{-1 + 2\sqrt{2}}$.

  • That puts the intersection point at $\br{-\frac{1}{3}, \frac{2}{3}\sqrt{2}}$, making the width of the upper triangle a third of the big triangle.

  • The big triangle has area $\sqrt{2}$, so the small triangle is a ninth of that, $\frac{1}{9}\sqrt{2}$.

A circle theorem? In the wild? Someone grab it!

Segment/tangent You might be forgiven for thinking, having heard me rant every so often, that I dislike circle theorems. That’s not true. In fact, I adore circle theorems. I just don’t think they have any place in a compulsory maths exam.

I even have a favourite! The intersecting chord theorem states that, if two chords AB and CD intersect at point P, then the products of the part-chords are equal: $AP \cdot PB = CP \cdot PD$.

Interesting thing: the same result holds, even if the crossing-point is outside the circle (and the chords are extended to become secants). It also holds even if one of the chords is, in fact, a tangent, with its endpoints in the same place.

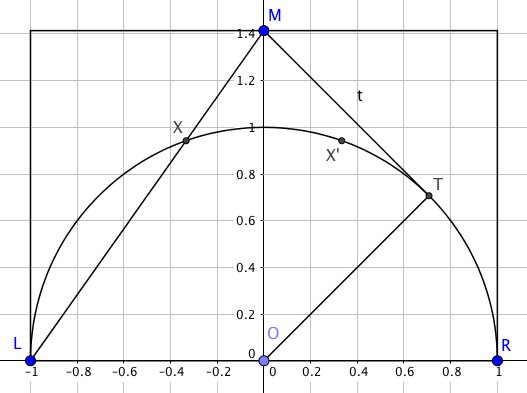
That’s the situation pictured here: the square of the tangent $TM$ is equal to the product $LM \cdot XM$.

Now, $TM$ takes a tiny bit of thought to figure out: triangle OTM is clearly right-angled at T; its hypotenuse is $\sqrt{2}$ and the leg $OT$ is 1 - so $TM=1$.

We know $LM$ from Pythagoras; it’s $\sqrt{3}$. The only thing we don’t know is $XM$ (let’s call that distance $x$). We have $\sqrt{3} x = 1$, so $x = \frac{\sqrt{3}}{3}$.

That means $XM$ is a third of the length of $LM$, and since triangle $LMR$ is similar to $XMX’$, the smaller triangle has a ninth of the area of the large one.

I think that’s a really elegant approach - but I’d be interested to see anything else that’s as neat!

* Many thanks to @srcav and @profsmudge for discussions on this problem.