Are you sure that's a right angle?
What’s that, @pickover? Shiver in ecstasy, you say? Just for a change.
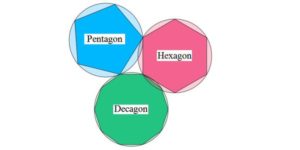
Shiver in ecstasy. The sides of a pentagon, hexagon, & decagon, inscribed in congruent circles, form [a] right triangle. pic.twitter.com/Uastgc7SJo
— Cliff Pickover (@pickover) May 20, 2017
That’s neat. But why?
Let’s suppose the circles all have radius 1, without loss of generality. Then the triangle’s side lengths are (in decreasing order) $2\sin\left( \piby 5 \right)$, $2\sin\left( \piby 6 \right)$ and $2\sin\left( \piby {10} \right)$.
Those will form a right-angled triangle if $\sin^2\left( \piby 5 \right) = \sin^2\left( \piby 6 \right) + \sin^2\left( \piby {10} \right)$. And… well, is it?
Let’s consider $Z = \sin^2\left( \piby 5 \right) - \sin^2\left( \piby 6 \right) - \sin^2\left( \piby {10} \right)$, which ought to end up as 0 to give us a right angle.
My first thought is, I don’t much like those $\sin^2$s. They’d be much nicer if they were $\cos$s. Luckily, there’s an identity: $2\sin^2(x) \equiv 1- \cos(2x)$.
If we double everything, that makes it a bit easier:
$Z = 1 - \cos\left(\frac{2}{5}\pi\right) - 2 + \cos\left(\piby 3\right) + \cos\left(\piby 5 \right)$
And of course, we know that $\cos\left(\piby 3\right) = \frac {1}{2}$, so we can tidy up:
$Z = -\frac{1}{2} + \cos\left(\piby 5 \right) - \cos\left(\frac{2}{5}\pi\right)$. (*)
Now for the cosines
Now let’s have a look at $\cos\left(\piby 5 \right) - \cos\left(\frac{2}{5}\pi\right)$. I shall call that $H$.
Using the cosine difference formula, $H = 2 \cos\left(\frac{2}{5}\pi\right)\cos\left(\piby 5\right)$.
Squaring the original $H$ gives $H^2 = \cos^2\left(\piby 5\right) - H + \cos^2\left(\frac{2}{5}\pi\right)$.
Doubling everything, as is normal procedure when $\cos^2$s show up: $2H^2 + 2H = 2\cos^2\left(\piby 5\right) + 2\cos^2\left(\frac{2}{5}\pi\right)$.
However, we know that $2\cos^2(x) = \cos(2x)+1$, which gives:
$2H^2 + 2H = \left(1+ \cos\left(\frac{2}{5}\pi\right)\right) + \left(1 + \cos\left(\frac{4}{5}\pi\right)\right)$.
Meanwhile, $\cos\left(\frac{4}{5}\pi\right) = - \cos\left(\piby 5\right)$, so the right hand side becomes $2 - H$.
We end up with $2H^2 + 3H - 2 = 0$, which factorises nicely as $(2H-1)(H+2)=0$, so $H = \frac{1}{2}$ or $H= -2$. Since the component parts of $H$ are both smaller in magnitude than 1, $H = \frac{1}{2}$ is the only sensible answer.
Argh! A Ninja!
“Roots of unity!” hissed the Mathematical Ninja. “$2\cos\left(\frac{2}{5}\pi\right) + 2\cos\left(\frac{4}{5}\pi\right) + 1 = 0$ so $2\left( \cos\left(\frac{2}{5}\pi\right) - \cos\left(\frac{1}{5}\pi\right)\right) = -1$. That’s $-2H = -1$. Would you like a tombstone?”
“Uh…”
”$\blacksquare$.”
“Thank you.”
So, where were we?
Oh yeah! Going back to (*), we’ve got $Z = -\frac{1}{2} + H$, so $Z = 0$ and our triangle is right-angled. Phew!
That might make one shiver in ecstasy, I suppose, if one were so inclined.
* Many thanks to @dragon_dodo who got the hard bit of the proof and then invited the Ninja in.