Some puzzles from Cav
A couple of puzzles that came my way via @srcav today:
Cav’s solutions to this one are here; mine are below the line further down.
Interesting angle puzzle https://t.co/UN13XwwY3o pic.twitter.com/NyaQL0H7wE
— Cav (@srcav) July 8, 2019
Have a go yourself before you read on!
I’ve mentioned before about @solvemymaths and @cshearer41 puzzles: they usually consist of two puzzles. First, finding an answer; secondly, finding a method that makes you go ‘oo!’.
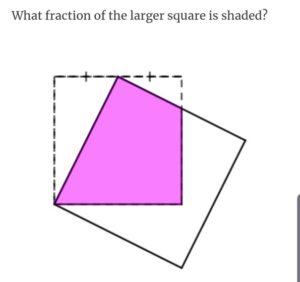
Area 48
- The white triangle at top-left is $\frac{1}{4}$ of the smaller square.
- The white triangle at top-right is $\frac{1}{16}$ of the smaller square (similar triangles)
- So the pink shape is $\frac{11}{16}$ of the smaller square.
- The larger square has side length $\frac{\sqrt{5}}{2}$ as long as the smaller square (via Pythagoras)
- So its area is $\frac{5}{4}$ as large.
- Therefore, the pink shape is $\frac{11}{16} \div \frac{5}{4} = \frac{11}{20}$ of the larger square.
Angle puzzle
My first thought, faced with this, was “I really can’t be bothered chasing all those angles. Surely there’s some symmetry to exploit?”
Surely there is.
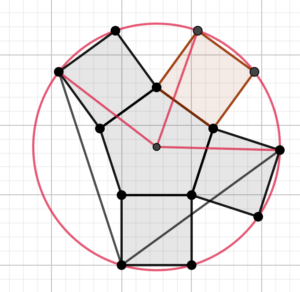
- All of the points on the outside of the squares lie on a circle (by symmetry). This circle has the same centre as the one going through the points of the pentagon.
- The red lines divide the angle at the centre of the circles into fifths - so the angle between the two outer red lines is thus $\frac{4}{5}\pi$.
- The angle subtended at the circumference yadda yadda - the angle between the two black lines is $\frac{2}{5}\pi$.
- So the original shaded angle is $\frac{8}{5}\pi$ (or 144 degrees, if the Ninja isn’t looking).
Nice puzzles!