How to pick a price for an e-book
A reader asks about e-book pricing:
“What’s the best price – mathematically – to sell my e-book at?”
This, my friends, is a thorny, thorny question. It’s lucky I’m a mathematician, which means I can brush aside all sorts of difficulties about perceived value, psychology, price points and sales methods. Look at me, I’m practically an economist! [caption id=”attachment_975” align=”alignright” width=”300”]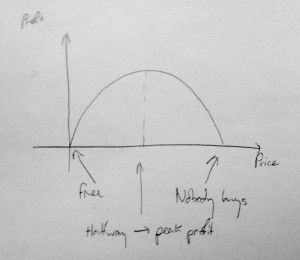
You get the best profits in the middle of the price range.[/caption]
TL;DR version
Here’s a recipe to find the your optimal e-book pricing:
- Find the highest price you can imagine anyone paying for your book
- Halve it
That’s it. Look at the graph.
What you just did there was applied calculus.
Seriously.
Now, I hinted before about some assumptions. Before all the marketing people, the ones who religiously read my blog, descend on me and say ‘e-book pricing isn’t really like that!’, I hear your objections. And I’m going to ignore them, because the beauty of maths is partly about starting from an ok-but-not-quite-right model and gradually refining it. (See also Newton=>Einstein, Lamarck=>Darwin, Early woo=>science).
What I’ve assumed is that people buy based solely on price. You’ll get the most ‘sales’ if you make it free (although you won’t make any money). I’ll call that number of sales $S$, for sales.
If you make it super-expensive, no-one at all will buy it. I’m going to call the highest price someone will pay, the highest possible price, or $H$.
I’ve also assumed that in between free and $H$, the sales are proportional to the discount((There must be an eleganter way to say that.)) – by which I mean, if you sell your books at $\frac{1}{3}$ off of H, you’ll get $\frac{1}{3}$ of the maximum number of buyers, and so on.
Look out, there’s an equation coming!
It’s ok, I do the sums so you don’t have to.
Your profit, if you sell the book at a given price $x$, turns out to be the number of buyers multiplied by the price they pay. I’m just going to magic that equation up:
$Profit = Sx(H-x)$
That’s the curve in the picture, by the way: you can see that if $x = 0$ (free), you make no money, and if $x = H$ (the highest possible price), you also get zero profit.
We don’t want to make no stinkin’ money, though; we want to get the most money possible - which is where the curve goes flat. And you find out how steep a curve is by differentiating. Don’t worry about how.
$gradient = S(H - 2x)$
For the curve to be flat, the gradient has to be zero:
$S(H - 2x) = 0$
And you can see that that can only be true if either $S=0$ (which means nobody buys your book when it’s free – which might be true of a maths book, I suppose) or if $x = \frac{H}{2}$ – half of the maximum possible price. That’s the optimal number for e-book pricing.
QED
You’re welcome to argue with the assumptions – please do that in the comments below – and next time I’ll show you how to price up something that has limits on, like your time, or the 100 physical books you have lying around.