Ask Uncle Colin: Simultaneous Trigonometry
Dear Uncle Colin,
I’m normally pretty good at simultaneous equations, but I can’t figure out how to solve this for $a$ and $b$.
$\cos(a)-\cos(b) = x$ $\sin(a)-\sin(b) = y$
- Any Random Circle
Hi, ARC, and thanks for your message!
This is, it turns out, a bit trickier than it looks at first glance - and (in most cases) unlikely to lead to exact answers.
So, rather than get to an explicit answer, I’ll talk through a strategy.
Draw a picture
Before anything else, we should draw a picture of what we’re looking at, using the geometric definitions of sine and cosine:
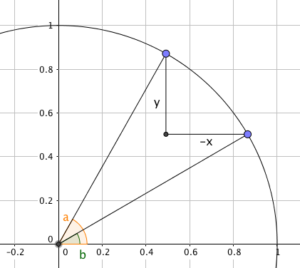
Play ‘spot the triangle’
The right-angled triangle shown, with legs of $-x$ and $y$, clearly has a hypotenuse of $\sqrt{x^2 + y^2}$.
The triangle comprising the origin and the two points is isosceles, with an apex angle of ${a-b}$ and two sides of length 1 while the other is $\sqrt{x^2 + y^2}$.
Splitting that in half tells us that $\sin\left(\frac{a-b}{2}\right) = \frac{\sqrt{x^2 + y^2}}{2}$.
The angle between the ‘$y$’ leg and the hypotenuse is $\frac{b+a}{2}$ after a little bit of algebra - which leads to $\sin\left(\frac{a+b}{2}\right) = \frac{-x}{\sqrt{x^2+y^2}}$.
Watch for the booby trap!
The temptation is to reach for a formula - possibly $\sin(A) + \sin(B) = 2\sin\left(\frac{A+B}{2}\right)\cos \left(\frac{A-B}{2}\right)$, but this will just lead you back to where you started.
Not that I did that, or anything, you understand.
It’s a bit cloggy
Instead, the best approach I have is to find the arcsine of both of the bits we’ve worked out, taking great care to ensure that they’re consistent with the signs of $x$ and $y$.
Adding the resulting angles together gives $a$; subtracting them gives $b$. Writing them out gives an unholy mess, and I’m not going there!
Hope it helps all the same,
- Uncle Colin
* Edited 2017-10-11 to correct the apex angle. Thanks to @evariste1832 for pointing out the error.