Ask Uncle Colin: Shouldn't this be simple?
Dear Uncle Colin,
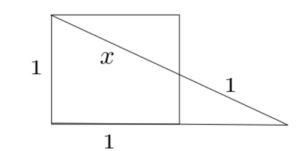
I’ve got a funny square and I can’t find $x$. Can you help?
- Oughta Be Simple, Can’t Unravel Resulting Equations
Hi, OBSCURE, and thanks for your message! You’re right, it ought to be simple… but it turns out not to be.
It is simple enough to set up some equations.
The sine of the ‘big’ triangle’s bottom-right angle is clearly $\frac{1}{x+1}$.
The cosine of the top-left angle of the medium triangle (the one with the right-angle in the top-right, and which is similar to the big triangle) is $\frac{1}{x}$.
Those two angles are the same, which means $\left(\frac{1}{x+1}\right)^2 + \left( \frac{1}{x} \right)^2 = 1$.
Tidying up
Multiplying everything by the denominators gives:
$x^2 + (x^2 + 2x + 1) = x^2(x^2 + 2x+ 1)$
This simplifies to
$0 = x^4 + 2x^3 - x^2 - 2x - 1$.
Ah, a quartic. My old nemesis! We meet again.
Some ingenuity
I don’t know (apart from numerically and via Wolfram) how to solve quartics, although I ought to. However, I have an idea: how about I try to get rid of the $x^3$ term by using a substitution?
If I let $x = y - \frac{1}{2}$, what happens? Well, after a horrible bit of algebra, I get $y^4 - \frac{5}{2}y^2 - \frac{7}{16} = 0$. What do you know? It turned into a quadratic!
Now I’ve got you
Multiplying by 16 for aesthetic reasons gives $16y^4 - 40y^2 - 7 = 0$. Completing the square tells me $(4y^2 - a)^2 + b \equiv 16y^2 - 40y - 7$, so $16y^2 - 8a + a^2 + b \equiv 16y^4 - 40y^2 - 7$. In the end, $a=5$ and $b=-32$.
So, $(4y^2-5)^2 - 32 = 0$, which gives $(4y^2-5) = \pm 4\sqrt{2}$, or $y = \pm \sqrt{ \frac{5}{4} \pm \sqrt{2}}$. For the second $\pm$, only the positive root makes sense, since $\frac{5}{4} < \sqrt{2}$.
Taking away the half again gives $x = -\frac{1}{2} \pm \sqrt{ \frac{5}{4} + \sqrt{2}}$. For the remaining $\pm$, only the positive root makes sense (or else we’d have a negative value for a distance.)
We end up with $x = -\frac{1}{2} + \sqrt{ \frac{5}{4} + \sqrt{2}}$ as the only positive real root of the equation - about 1.13, which looks plausible.
Oh look! The Mathematical Ninja!
“If you write that as $2x = -1 + \sqrt{5 + 4\sqrt{2}}$, it’s rather neater. $4\sqrt{2}$ is about 5.65, so we need the square root of $10.65$. That’s obviously about 3.25…”
“Obviously… ow.”
“More accurately, you say? 10.24 is $3.2^2$, so $3.25^2$ is 10.5625. Error is about 0.09, divided by 6.5, 0.18 over 13 is 0.01385 or so. So 3.264 seems better. Can I carry on now?”
“Yes, sensei.”
“Take away 1 to get 2.264 and halve the result. Hey presto: 1.132, as prophesied.”
Whoosh.
Phew! I hope that helps!
- Uncle Colin