Ask Uncle Colin: Incircles
Dear Uncle Colin,
I noticed that the incircle of a 3-4-5 triangle has a radius of 1, and for a 5-12-13 triangle, it’s 2. Is it always an integer in a Pythagorean triangle?
Having Elegant Radius Or Not?
Hi, HERON, and thanks for your message!
It turns out that yes, the incircle of a Pythagorean triple always has an integer radius. The key to the problem (for me, at least) is the equal-tangents theorem.
A picture
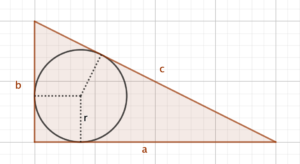
Looking at this diagram, you can see that the two tangents that meet at the right angle must have length $r$.
The other vertical tangent must have length $b-r$; the other horizontal tangent must have length $a-r$.
Because two tangents meeting at a point have equal length, the upper-left portion of the hypotenuse must also have length $b-r$, and the lower-right portion also $a-r$.
But, those two together make $c$, so $(b-r) + (a-r) = c$, which rearranges to $a+b - c = 2r$. (This is consistent with both of your observations).
But is $r$ an integer?
This isn’t quite enough: we still need to show that $a+b-c$ is even!
And it is, of course: because it’s Pythagorean - $a^2 + b^2 - c^2 \equiv 0 \pmod{2}$; meanwhile, $x^2 \equiv x \pmod {2}$, so $a + b - c \equiv 0 \pmod{2}$ - so it is indeed even, and the incircle radius is always an integer!
Hope that helps,
- Uncle Colin