Ask Uncle Colin: An absolute quadratic inequality
Dear Uncle Colin,
I have to solve the inequality $x^2 - \left|5x-3\right| \lt 2+x$. I rearranged to make it $x^2 - x - 2 \lt \left|5x-3\right|$ , but the final answer is eluding me.
-- Put Right Inequality Muddle
Hello, PRIM!
You’re off to a good start; the next thing I would do would be to sketch the two curves. Here’s Desmos’s version: 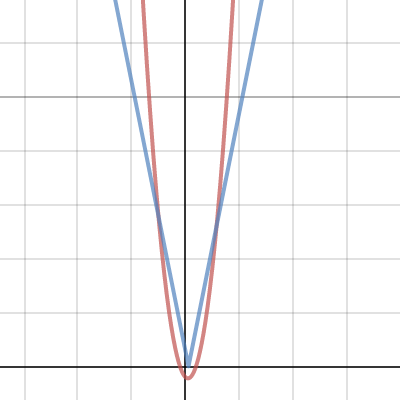
We want to know where the left-hand side (the curve) is below the right-hand side (the V). That’s clearly between the two crossing points; now all you need to do is find the crossing points!
On the right, the modulus graph is $y=5x-3$ (it’s sloping upwards, so it must be the version with the positive gradient). You need to solve $x^2 - x - 2= 5x - 3$, or $x^2 - 6x + 1 = 0$. That has roots at $3 \pm 2\sqrt{2}$, but the value you want is greater than $x = \frac{3}{5}$ because that’s where the point of the V is. You need the positive solution, which is $x = 3 + 2\sqrt{2}$.
On the left, the graph is $y = 3 - 5x$ and you need to solve $x^2 - x - 2 = 3 - 5x$, or $x^2 + 4x - 5 = 0$. That factorises as $(x+5)(x-1)=0$, and so $x=-5$ or $x = 1$. However, $x=1$ doesn’t fit with the graph (for this one, $x \lt \frac{3}{5}$), so the solution you want is $x=-5$.
That means the final answer you need is $-5 \lt x \lt 3 + 2\sqrt{2}$.
Hope that helps!
-- Uncle Colin