Ask Uncle Colin: A Fraction of a Square
Dear Uncle Colin,
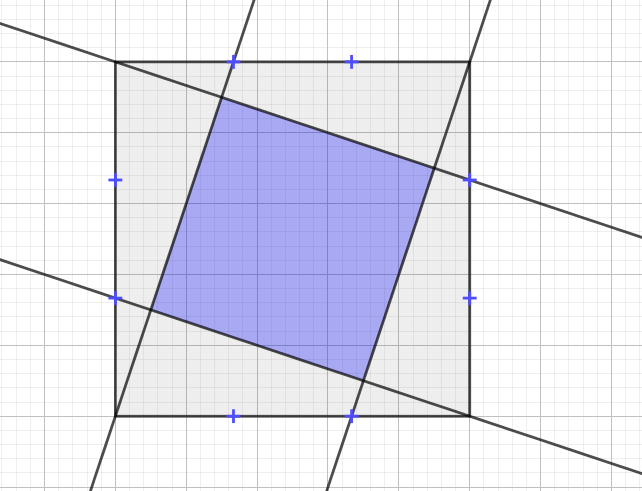
I have been presented with this diagram: the marked points are a third of the way along the sides. I need to know what fraction of the grey square is shaded blue. Any ideas?
Somehow Hued Area Defies Evaluation
Hi, SHADE, and thanks for your message!
There are several ways of doing this, some brutal and some more elegant.
Let’s do it a brutal way first.
Brutality!
Suppose the coordinates of the corners of the square are $(0,0)$, $(0,1)$, $(1,1)$ and $(0,1)$.
Then an equation of the line through the origin is $y=3x$, and an equation of the line through the top-left corner is $3y + x = 3$.
Substituting into the second gives us $10x = 3$, so one of the crossing points is at $(0.3, 0.9)$.
There are at least two ways to go here: symmetry can give us the other coordinates and we can Pythagoras the whole thing up. That’s a perfectly reasonable way to get the answer if you’re a computer scientist or something, but around here we value a little bit of elegance.
Instead of looking at the square, we can look at the triangle with its apex at $(0.3, 0.9)$ and its base along the left-hand side of the square. It has a ‘height’ (measured horizontally) of 0.3 and a base (vertically) of 1, so its area is 0.15.
That triangle is repeated four times around the edge of the blue square, making a total of 0.6 units squared, and the area of the square is therefore 0.4.
Elegance!
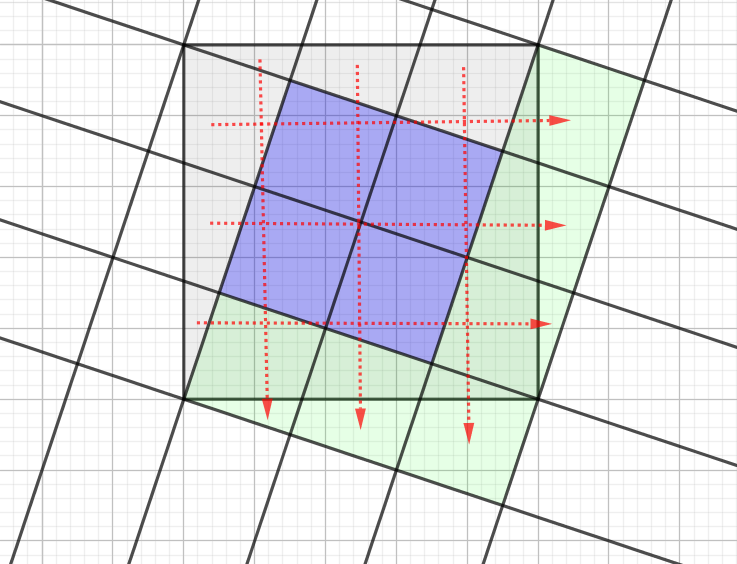
If I add in more parallel lines, splitting the shaded bit into four equal pieces, and jigsaw the outside pieces around to make congruent squares, I find there are six of those. So the blue area is two-fifths of the shaded area.
Hope that helps!