Ask Uncle Colin: A Circumcircle
Dear Uncle Colin,
I have a triangle with edge lengths of 9, 7 and 6 units. I need to find the area of the circumcircle. How do I do that?
Help! Euclidean Reasoning’s Off!
Hi, HERO, and thanks for your message!
I have a slightly cloggy method, and a possibly nicer one.
Get your clogs on
Here’s my picture: 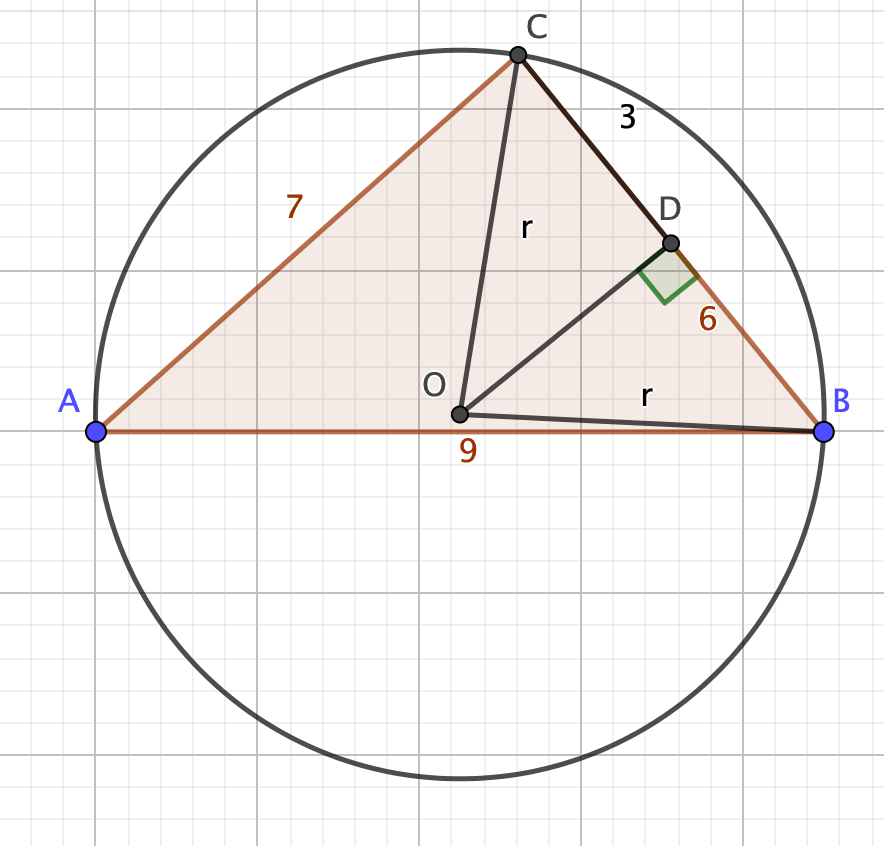
The plan of attack is to pick an angle of the triangle – I’m going for A, the one opposite the side of length 6 units – and find its cosine using the cosine rule.
I can then pick out the isosceles triangle OBC (angle BOC is 2A), and split it in half to get the right-angled triangle ODB. Angle DOB is equal to A, so $\sin(A) = \frac{3}{r}$.
From the cosine rule, $\cos(A) = \frac{9^2 + 7^2 - 6^2}{2(9)(7)} = \frac{47}{63}$.
Obviously, we could work out the angle, throw that back into the equations, and figure out $r$. But it’s more work than we need to do: we can just rearrange and find $r^2$ directly.
We have $\cos^2(A) + \sin^2(A) = 1$, so $\frac{3^2}{r^2} = 1 - \frac{47^2}{63^2}$.
That works out to $\frac{9}{r^2} = \frac{63^2 - 47^2}{63^2}$, so $r^2 = \frac{(3)^2(63)^2}{(16)(110)}$, using the difference of two squares.
The top is $189^2$, which is $(200 - 11)^2$, or $40,000 - 4,400 + 121$; that’s 35,721.
The bottom is 1760, so the area is $\frac{37,521}{1760}\pi$.
Whoosh
Hello, sensei, long time no see!
“You might not have seen me.”
I imagine you have a nice way to approximate that monster.
“Monster? Pah! The bottom is a multiple of 22 and the top is a multiple of 7, that’s a puppy-dog. The estimate is $\frac{5,103}{80}$, which is 63.8 or so.”
An insight
Alternatively, we know:
- The area, $T$, of the triangle is $\sqrt{s(s-a)(s-b)(s-c)}$, where $s$ is the semiperimeter
- It’s also $\frac{1}{2} bc \sin(A)$
- The diameter of the circumcircle is $\frac{a}{\sin(A)}$ (this is what the sine rule measures)
These give:
- $4rT = abc$
- $r^2 = \frac{(abc)^2}{16s(s-a)(s-b)(s-c)}$
Here, $s = \frac{9+7+6}{2} = 11$, so $r^2 = \frac{(9^2)(7^2)(6^2)}{16(11)(2)(4)(5)}$.
There’s a 4 to cancel, and we get $r^2 = \frac{189^2}{1760}$, as before.
Hope that helps!
- Uncle Colin
* Edited 2022-12-29 to add a missing picture.