An interesting GCSE triangle
It’s not often I have anything nice to say about EdExcel. I’ve usually found their exams to be the most predictable and least thought-provoking of all the boards (at least until they finally snapped in 2013 and let Kate the Photographer loose on an unsuspecting cohort).
At GCSE, their advanced trigonometry questions are usually as predictable as what Alexander Armstrong is going to ask you in the chit-chat section of Pointless: your triangle will be set up so you can blindly apply the sine rule, cosine rule or area formula more or less off the shelf. Three marks, next question.
This one is a bit more interesting. It’s not in the traditional “two pairs” format for sine rule, nor in the ‘elbow’ format for cosine rule – you’re going (shock! horror!) to need to do some thinking.
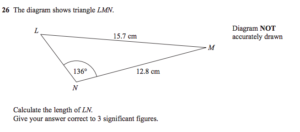
Here’s a triangle.
Side $LM$ is 15.7cm, $NM$ is 12.8cm, and angle $L\hat N M$ is 136º. While I think degrees are awful, they’re the angle currency at GCSE, so I’m stuck with them for this question.
I have two methods I’m happy with for it, but I’d love to hear others!
First method: sine rule twice
This is probably the simplest way to do it, although simple for me and simple for you aren’t necessarily the same. I would work out angle $L$ using the sine rule:
$\frac {15.7}{\sin(136º)} = \frac{12.8}{\sin(Lº)}$
A bit of pirate rearrangement gives: $\sin(Lº) = \frac{12.8 \sin(136º)}{15.7} \approx 0.566$, so $L \approx 34.5º$.
From there, you can establish that angle $M$ is about $9.5º$, because the interior angles in a triangle add up to 180º. Knowing that, you can apply sine rule again – being careful to use your Ans button rather than typing the number in again:
$\frac {LN}{\sin(9.5º)} = \frac{15.7}{\sin(136º)}$, giving $LN = \frac{15.7 \sin(9.5º)}{\sin(136º)} \approx 3.73$cm.
Using the cosine rule with an unknown
There’s another, possibly more tricky way, but it’s nice to see that maths all hangs together. Here, you can use the cosine rule, calling the unknown side $x$, and applying the quadratic formula to get the side length.
The cosine rule says: $15.7^2 = 12.8^2 + x^2 - 2 \times 12.8 \times x \times \cos(136º)$
Working out the numbers: $246.49 = 163.84 + x^2 + 18.42x$ – I’d keep hold of the exact answer to $2 \times 12.8 \times \cos(136º)$ in the calculator for later use.
Rearrange into a natural quadratic: $0 = x^2 + 18.42x - 82.65$
Don’t bother trying to factorise, put it straight into the equation: $x = \frac{-18.42 \pm \sqrt{18.42^2 + 4\times 82.65}}{2} = \frac{-18.42 \pm 25.88}{2}$
Only the positive answer makes sense, since it’s a distance – and you get 3.73cm again!
It’s always nice when two distinct methods give the same answer – and I’d be curious to know if you have any other ways to approach it!
* Edited 2015-10-26 to reassure readers I can count to two better than Bill can. Thanks, Eva, for the correction.