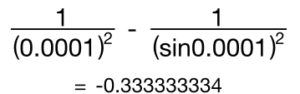Finding a limit

How would I find the limit of $\frac{1}{x^2} - \cosec^2(x)$ as $x$ goes to 0?

There are several valid approaches to this; two that spring to mind are L’Hôpital’s rule, which I like because it’s got an accent and two apostrophes, and series expansions, which I like because I like them, ok?

In both cases, the first step is to turn the expression into a single fraction: $\frac{\sin^2(x) - x^2}{x² \sin^2(x)}$.

If you try putting $x=0$ into that fraction, you get… a problem. The top is 0 and the bottom is 0, which is an indeterminate form - you need to do more work.

L’Hôpital’s Rule

L’Hôpital’s Rule was discovered by Bernoulli, of course, and says “if you have an indeterminate limit of the form $\frac{f(x_0)}{g(x_0)}$, the limit is given by $\frac{f’(x_0)}{g’(x_0)}$.”

Unfortunately, in this case, the first derivatives are both zero. As are the second derivatives. And the third. Not to mention the fourth. It’s a real bear to get down to something you can work with – five pairs of derivatives, each nastier than the one before.

Let’s do it the other way.

Series expansion

In your trusty formula book, you’re told that $\sin(x) \approx x - \frac 16 x^3 + O(x^5)$ - the big O means “stuff that’s this small or smaller” - when we’re looking at small values of $x$, it saves us thinking about really really small ones!

If we square that, carefully, we get $\sin^2(x) \approx x^2 - \frac 13 x^4 + O(x^6)$.

The top of the fraction becomes ${-\frac 13 x^4 + O(x^6)}$. (Yes, I changed the sign of the big O thing. Doesn’t matter. We’ll treat it as 0 in a minute).

The bottom of the fraction becomes $x^4 + O(x^6)$.

Dividing both top and bottom by $x^4$ gives $-\frac 13 + O(x^2)$, which goes to $-\frac 13$ as $x$ goes to 0.

Calculator check

Boom.