Eye to Eye
A nice observation from Futility Closet:
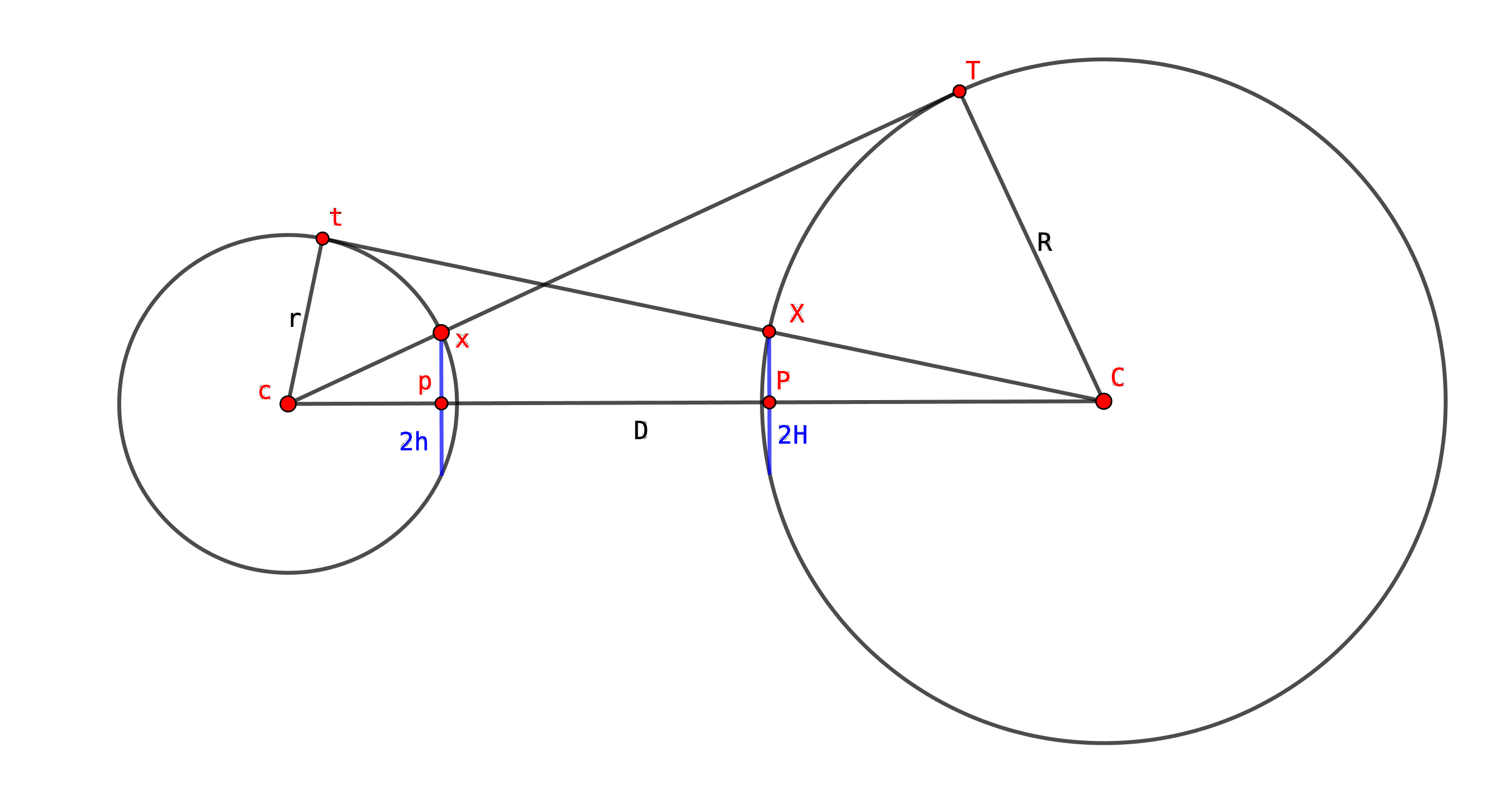
Draw two circles of any size and bracket them with tangents, as shown.
The chords in blue will always be equal.
I’m hardly going to let that pass by without a proof, now, am I? Spoilers below the line.
My proof
- Definitions
- Let the distance between the centres be $D$.
- Let the radius of the left-hand circle be $r$ and that of the right-hand circle be $R$. Let their respective centres be $c$ and $C$.
- Let the length of the left-hand blue line be $2h$ and that of the right-hand blue line be $2H$. (I’ve put the 2 in because I’m going to halve them shortly.)
- Let the upper points of tangency be $t$ on the left circle and $T$ on the right circle.
- Let the upper points where the blue chords meet their circles be $x$ on the left and $X$ on the right.
- Observations
- The left-hand blue chord crosses $cC$ at right angles; let the point where it does this be $p$.
- Similarly for the right-hand blue chord; let its crossing-point on $cC$ be $P$.
- Triangle $cxp$ is right-angled at $p$, and is similar to triangle $cCT$ - so $\frac{h}{r} = \frac{R}{D}$ [1].
- Similarly, $CXP$ is right-angled at $P$, and is similar to $CcT$ - so $\frac{H}{R} = \frac{r}{D}$ [2].
- Conclusion
- From [1], $h = \frac{rR}{D}$
- From [2], $H = \frac{rR}{D}$
- So $h=H$ and the two chords are equal.
* Edited 2020-08-17 to improve the diagram and change some colours. Thanks, Barney!